Güneşin doğuş zamanının hesaplanması:
4 Mayıs 1999 günü 38 derece N – 026 derece E mevkiinde bulunan bir gözlemci için Güneş’ in doğuş zamanı UT ( GMT ) nedir? ( Ek cetveller 07 – 08 – 38 – 39 )
Çözüm: ek cetvel 38’ e gir N 35 – 40 derece enlemler arasındaki güneşin doğuşu çizelgesinden değerleri al;
40 à 04.56 35à 05.06 Aradaki farkı bul; dlat= 5 derece =05.06 – 04.56= 10 dakika
38 – 35 = 3 derece fark var. 5 derece 10’ ise 3 derecede dlat 6’ eder
Ek cetvel 8 de enlem çizelgesine gir 5 derece sütunundan 3 derece yi bul ve onun sırasından 10 dk, sütunundaki değeri al. ( 6 ‘ ) Zaman farkı 6 dakika. 10 5 2 5’ 10’ 15’
3à 6’
Enlem değeri büyüdükçe zaman değeri eksildiği için 6 dk, 35 derece karşılığı zaman değeri olan 05.06 dan çıkarılacak. Lat 35 N 05.06’ – Lat 38 N – 06’= 05.00 LMT
26 derece E boylamı için ek cetvel 7’ ye gir ( 0 – 59 dereceler ) arası 26 derece karşılığını bul; 1h44m. Doğuda bulunulduğu için bulunan değer 05.00 LMT den çıkarılacak.Cevap; 05.00 – 1.44= 3h.16m
Güneşin batış zamanının hesaplanması:
04 Mayıs 1999 günü 42 derece N – 039 derece E mevkiinde bulunan bir gözlemci için Güneşin batış zamanı UT ( GMT ) nedir? ( ek cetvel 07 – 08 – 38 – 39 )
Ek cetvel 38 e gir Güneşin batışı bölümünden 40 – 35 derece enlemleri arasındaki zaman değerlerini al. 45à 19.10 40à 18.58 aradaki farkı bul; 19.10 – 18.58= 12 dk, dlat= 5 derece
45-42= 3 derece.
Ek cetvel 8 e gir 5 derece sütunundan 3 dereceyi bul ve 3 derece sütunu karşılığı dk, bölümünden 12 dk için 10’ ve 15’ değerlerini al 10 5 2 5’ 10’ 15’
3à 6’à 9’
10’ için 6’ fark varsa 12’ için nedir? 12×6/10=7.2 7.2= -7×60=12” saniye.=7’.12”
Lat 45Nà 19.10’ – Lat 42Nà 07’12”= 19.02’.48”
Ek cetvel 7 ye gir derecenin zamana çevrilmesi çizelgesinden ( 0 – 59 ) sütun undan 39 derece boylamının karşılığını bul. ( 2.36’ ) E yani doğuda bulunulduğu için LMT den bulunan değerleri çıkar.
Cevap; 19.02’48” – 2.36’= 16h26m48s
Sabah Sivil alaca karanlık hesaplanması:
05 Mayıs 1999 günü 39 derece N – 007 derece E mevkiinde bulunan bir gözlemci için sabah sivil alaca karanlık zamanı UT ( GMT ) olarak nedir? ( ek cetvel 07 – 08 – 38 )
Ek cetvel 38 e Güneşin doğuşu bölümünden gir 35 ve 40 derece enlem sütununun karşısındaki sivil alacak karanlık değerlerini al.
Lat 35à 04.38’ Lat 40à 04.26’ dlat= 5 derece. 40 – 39 = 1 derece fark. 04.38’ – 04.26= 12’ fark
Ek cetvel 8 e gir 5 derece için 1 derece karşılığını bul onun sırasındaki dakika sütunundan 10’ ve 15’ değerlerini al. 10 5 2 5’ 10’ 15’
1à 2’à 3’
10’ için 2’ ise 12’ için nedir? 12×2/10= 2’24 2.’24= -2×60= 24” = 2’.24”
Enlem değerleri azaldıkça zaman değeri büyüdüğü için çıkan değeri Lat 40 zaman değeri ile toplarız.
04.26’ + 2’24”= 04.28’ 24”
007 E derecesini zamana çevirmek için Ek cetvel 7 ye gir ( 0 – 59 ) sütunundan 007 derece karşılığını bul. ( 0.28’ ) boylam E olduğu için LMT den çıkarılır. Cevap; 04.28’24” – 0.28’= 04.00’ 24”
Akşam sivil alaca karanlık hesaplanması:
04 Mayıs 1999 günü 24 S – 017 W mevkiinde bulunan bir gözlemci için akşam sivil alaca karanlık zamanı UT ( GMT ) nedir? ( Ek cetvel, 07 – 08 – 38 – 39 )
Ek cetvel 38 de güneşin batışı bölümünden 20S ve 30S derece enlem sütunu karşısındaki sivil alacak karanlık değerlerini bul.
Lat 20Sà 17.59’ Lat 30 Sà 17.47’ dlat= 10 derece zaman farkı = 17.59 – 17.47= 12’ dk.
24S – 20S= 4 derece fark.
Ek cetvel 8 e gir 10 derece sütunundan 4 dereceyi bulà onun karşılığı dakika sütunundan 10’ ve 15’ değerlerini bul. 10 5 2 5’ 10’ 15’
4à 4’à 6’
10’ 4 ‘ ise 12’ nedir? 4×12/10=4.8 4.8= -4 x60=48” = 4’48”
Güneyde enlem değeri arttıkça zaman değeri azaldığı için bulunan değer Lat 20 S zaman değerinden çıkarılacak. Lat 20Sà 17.59’00” – 4’48”= 17.54’12” LMT
17W boylamı için Ek 7 çizelgesine gir ( 0 – 59 ) boylam sütunundan 17 derece için zamanı bul. 17= 1h08dk. Bulunan değeri boylam W olduğu için LMT ile topla. 17.54’12” + 1.08’00”= 19.02’12”
Cevap: GMT: 19.02’12”
Ayın GHA ve Dec değerleri hesaplanması:
04 Mayıs 1999 günü 02h24m00s GMT de ayın GHA ve Dec değerleri nedir?( ek cetvel 13 – 38 )
Ek cetvel 38 e gir 04 Mayıs günü 02 GMT de Ay sütunundan Ayın GHA – v – Dec ve d değerlerini bul.
GHA v Dec d
02 00 00 351.02’8 12.2 S18.56’9 3.3
24 00 5.43.6
V 5.0 d 1.3
GHA 356.51.4 Dec S18.58.2
Ek 13 e gir ( artmalar ve düzeltmeler çizelgesi ) 24 dakika çizelgesinden 00 saniye için karşılığı Ay için olan değeri al. 5.43’6. gene 24 dk çizelgesinden v ( 12.2 ) düzeltmesi için değeri al. 12.2à5.0 d ( 3.3 ) için görülen değerleri al. 3.3à 1.3 bulunan değerleri GHA ve Dec değerlerine ekle.
Cevap: GHA: 356.51.4 Dec: S18.58.2
Ayın GHA ve Dec değerlerinin hesaplanması
03 Mayıs 1999 günü 04h 25m15s GMT de Ay ın GHA ve Dec değerleri nedir. ( ek cetvel 13 – 39 )
Ek cetvel 39 a gir 03 Mayıs saat 04 için Ay sütunundan Ayın GHA – v – Dec ve d değerlerini bul.
GHA v Dec d
04 00 00 031.27’3 12.9 S17.22.6 5.1
25 15 6.01’5
V 5.5 d 2.2
GHA 037.34’.3 Dec S17.24’8
Ek cetvel 13 e gir 25 dakika bölümünden 15s karşılığı değeri bul. 15à6.01.5 v (12.9 ) karşılığını bul 12.9à5.5. d( 5.1 ) düzeltemesi için karşılığını bul 5.1à2.2 Bulunan değerleri GHA ve Dec değerlerine ekle.
Cevap: GHA: 037.34.3 Dec: S17.24’8
Ayın GHA ve Dec değerlerinin hesaplanması
03 Mayıs 1999 günü saat 20h 24m 48s ZT da 48.00 N 020.30 E mevkiinde ayın GHA ve Dec değerleri nedir? ( ek cetvel 13 ve 39 )
Çözüm: ZD= -1 GMT = ZT – ZDà GMT= 20.24’.48”- 1 = 19h 24m.48s bulunur. ( boylam 20 E olduğu için değer ( – )
Ek 39 a gir 03 Mayıs için Ay sütunundan saat 19.00 için Ay ın GHA v Dec ve d değerlerini bul.
GHA v Dec d
19 00 00 249.23’0 12.5 S18.31’2 3.9
24’48” 5.55’1
V 5’1 d 1’6
GHA 255.23’2 Dec S18.32’8
Ek cetvel 13 e gir 24 m sütununda 48 s için değeri bul 48à 5.55’1. Gene aynı sütundan v ( 12.5 ) değeri düzeltme karşılığını bul.12.5à 5.1 d ( 3.9 ) karşılığını bul. 3.9à 1.6 bulunan değerleri GHA ve Dec değerlerine ekle.
Cevap: GHA: 255.23’2 Dec: S18.32.8
Güneşin GHA ve Dec değerlerinin hesaplanması
03 Mayıs 1999 günü saat 16h 25m 38s ZT’ da 40.45’N – 029. 35’E mevkiinde Güneşin GHA ve Dec değerleri nedir?
Çözüm: ZD – 2. GMT= ZT -/+ ZD à GMT= 16h25m 38s – 2h= 14h 25m 38s GMT: 14h 25m 38s
Ek cetvel 39 a gir Güneş sütunu 3 Mayıs saat 14 00 için GHA, Dec ve d değerlerini al.
GHA Dec d
14 00 00 30.46’6 N15.38.9 0.7
25 38 6.24’5 d 0.3
GHA 37.11.1 Dec N15.39.2
Not cevapta. GHA 37.11.1 Dec N15.38.6 gözüküyor. Normalde zaman değeri arttıkça GHA ve Dec değerleri artığı için ( + ) olması gerekir. Zaman değeri arttıkça değerler düşüyorsa o zaman ( – ) olur.
Ek cetvel 13 e gir 25m sütunundan 38 s için değerleri al. 38sà 6.24’5. d ( 0.7 ) düzeltme değerini alà 0.3 bulunan değerleri GHA ve Dec değerine ekle
Ay ın üst meridyenden geçiş hesaplanması
05 Mayıs 1999 günü 42 N – 028 W mevkiinde bulunan bir gözlemci için Ayın üst meridyenden geçiş zamanı nedir? ( ek cetvel 7 – 8 ve 38 )
Çözüm: Ek cetvel 38 e gir sağ alt köşeden Ay ın meridyen geçiş bölümünden 5 Mayıs ve 6 Mayıs değerlerini bul
5 Mayısà 03.25 6 Mayısà 04.14 aradaki farkı bul. 04.14 – 03.25= 49 dakika.
Ek cetvel 7 ye gir 28 w boylamının saat değerini bul. 28Wà 1h 52m. Boylam işareti W olduğu için 03.25 zaman değeri ile + ( 03.25 + 01.52= 05.17 )
Ek cetvel 8 e gir II çizelgeden 28 W boylamı için 49 dakika değerini bul. ( 28 W ve 49m için yaklaşık değer 20 derece ve 50m olduğu için onların değerleri alınacak )28à 50à 4 m bulunan değeri boylam işareti W olduğu için 05.17 ye ekle. 05h17m + 4m= 05h21m. Cevap 05h21m
Ayın üst meridyenden geçiş hesaplanması
05 Mayıs 1999 günü 37 N 025 E mevkiinde bulunan bir gözlemci için Ay ın üst meridyenden geçiş zamanı UT ( GMT ) nedir? ( ek cetvel 7 – 38 )
Ek cetvel 38 e gir sağ alt köşeden Ay ın meridyen geçiş bölümünden 4 ve 5 Mayıs için değerleri bul.
Ek cetvel 7 ye gir 025 derec E boylamının zaman değerini bul. 025à 1h 40m
Bulunan değeri 03.25 den çıkar. 03.25 – 01.40= 01.45
Not: burada normalde ek cetvel 8 de verilmesi gerekir ve doğu boylamı olduğu için bir önceki tarih yani 04 mayıs değeri de alınması gerekir. 05 mayıs değeri arasındaki zaman farkı bulunup ek cetvel 8e giriş yapıp bulunan değer 01.45 ten boylam doğu olduğu için çıkarılması gerekir.
04 Mayıs 02.37 03.25- 02.37= 48 dakika fark. Ek cetvel 8 den 25 Eà 48 karşılığı bulunur (3’,5 = 4’) bulunan değer 01.45 ten boylam E olduğu için çıkarılır. 01h45m – 4m= 01.41 doğru cevap. Fakat şıklarda yok.
Güneşin meridyenden geçişi hesaplanması
05 Mayıs 1999 günü 36.20’N – 032.42’ E mevkiinde bulunan bir gözlemci için Güneşin meridyenden geçiş zamanı UT ( GMT ) nedir? ( ek cetvel 7 – 38)
Ek cetvel 38 sağ alt köşeden Güneş in üst meridyen geçişini bul. à11.57
Ek cetvel 7 ye gir ( 0 – 59 ) çizelgesinden 32 E boylamının zaman değerini bul 32à2h 08m
Ek cetvel 7 de 42m için değeri bul 42à 2’48” bulunan değerleri topla. 2h08m+2m48s= 2h10m48s
Bulunan değerleri boylam E olduğu için Meridyen geçişinden çıkar ( – ) 11h57m00s – 2h10m48s=09h 46m12s Cevap: 09h46m12s
Güneşin meridyenden geçiş hesaplanması.
02 Mayıs 1999 günü 22.10’S 046.18’W mevkiinde bulunan bir gözlemci için Güneşin meridyenden geçiş zamanı UT ( GMT ) nedir? ( ek ctvel 7 ve 39 )
Ek cetvel 39 a gir sağ alt köşeden Güneşin meridyen geçiş zamanını bulà11.57
46 W boylamı için ek cetvel 7 ye gir ( 0 – 59 ) sütunundan 46 W için zaman değerini bulà3h04m ek cetvel 7 de 18m için değeri bulà1m12s bulunan değerleri topla 3h04m+1m12s= 3h05m12s
W boylamında bulunulduğu için bulunan değeri Güneşin meridyenden geçiş zamanına ekle ( + )
11H57m + 3h05m12s=15h02m12s Cevap: 15h02m12s
Pollux yıldızı meridyen geçişi hesaplanması.
05 Mayıs 1999 günü 43 N – 036 E mevkiinde bulunan bir gözlemci için Pollux yıldızının meridyen geçiş zamanı UT ( GMT ) olarak nedir? ( ek cetvel 7 ve 42 )
Çözüm:Ek cetvel 42 ye gir; Pollux SHA= 243 41’3 bulunan değeri 036 E boylamı ile topla
243.41’3+036=279.41’3 GHA ( Aries )= 360 – 279.41’3= 80.18’7= 80.18’42” ( 7×6=42”)
Ek cetvel 42 de Aries in 5 Mayıs sütununda 80.18’42” ile gir. Zaman olarak 1400 ve 1500 arasına denk gelir. Bu zamanların GHA değerlerini al ve aradaki farkı bul.
1400 72.59’9
1500 88.02’4 88.02’4 – 72.59’9= 15.02’5=15.02’30” ( 5×60=30”) aradaki fark: 15.02’30”
80.’18’42” ( 42” / 6 = 7 ) aradaki farkı bulmak için saniye yi ondalığa çevirmek gerekir. 80.18’7
72.59’9 aradaki fark 80.18’7 – 72.59.9= 07.18’8 ( ondalığı saniye ye çevir 8×6 48”= 07.18’48”
Ek cetvel 7 ye gir 7 derece karşılığını bulà 0.28’ ek cetvel 7 de 18’ karşılığını bulà 1’12” bulunan değerleri topla 28’+1’12”=29’12” bulunan bu değeri saat 1400 e ekle 1400’ + 29’12”=14.29’12”
Cevap: 14h29m12s Soru cevabı 14.29.10
Rigel yıldızının meridyenden geçiş zamanı hesaplanması
06 Mayıs 1999 günü 35 S – 052 W mevkiinde bulunan bir gözlemci için Rigel yıldızının meridyenden geçiş zamanı nedir? ( ek cetvel 7 ve 42 )
Ek cetvel 42 ye gir rigel yıldızının SHA değerini bulà 281.22’9 boylam W olduğu için bulunan Sha değerinden çıkar. 281.22’9 – 52 = 229.22’9
GHA Aries = 360 – 229.22’9 = 130.37’1 bulunan değer ile 6 mayıs sütunundan Aries GHA değerine gir. Girilecek bölüm zaman olarak 1700 ve 1800 zaman aralıkları.
1700 GHA= 119.06’4
1800 GHA= 134.18’9 aradaki farkı bul; fark = 15.12’5
130.37’1 ile 1700 Aries GHA arasındaki farkı bul; 130.37’1 – 119.06’4= fark. 11.30’7
Ek cetvel 7 ye gir 11 derece için ( 0 – 59 ) sütunundan zaman değerini bulà 0.44’. 30’ için değeri bulà2’00” bulunan değerleri topla 0.44’+2’.00= 0.46’
Bulunan değeri saat 1700 aries zamanına ekle = 17.00 + 0.46= 17.46’00”
Not soru cevabında 17 45 55 gözüküyor.
Alphard yıldızı GHA ve Dec değerlerinin bulunması.
02 Mayıs 1999 günü 17h 25’ 26” ZT da 30.09’ N – 078.45’ W mevkiinde Alphard yıldızının GHA ve Dec değerleri nedir? ( ek cetvel 13 – 44 )
ZDà 78à 78/15=5h12m ZD ( W ) +5 olduğu için
GMT= ZT +/-ZDà 17h25m26s + 5h= 22h25m26s GMT olur.
Alphard SHA 218.06’8 Dec S8.39’5
2 Mayıs 1999 için saat 22 00 Aries GHA 190.22’2
Ek cetvel 13 e gir 25m sütunundan 26 saniye için değeri bul 25à 26à aries değeri 6.22’5 bulunan değeri Aries GHA ya ekle 190.22’2 + 6.22’5 = 196.44’7
Bulunan değeri Alphard SHA ile topla. 196.44’7+ 218.06’8= 414.51’5 değer 360 dereceden büyük olduğu için 360 dereceden çıkar 414.51’5 – 360= 054.51.5
Cevap: GHA 54.51’5 Dec.S8.39’5 Soru cevabı; 24.46’6 – S8.39’5 gözüküyor.
Capella yıldızının GHA ve Dec değerleri bulunması
06 Mayıs 1999 günü 06 24 37 UT ( GMT ) de Capella yıldızının GHA ve Dec değerleri nedir.( ek cetvel 13 ve 42 )
Çözüm: GHA ( yıldız ) = GHA ( Aries ) + SHA ( yıldız )
Ek cetvel 42 ye gir 6 mayıs 0600 için Aries sütunundan aries in 0600 GHA değerini alà Aries GHA =313.39’3. Ek cetvel 42 de Capella yıldızının SHA ve Dec değerlerini al. SHA 280.51’1 Dec.N45.59’8
GHA ( Aries ) + SHA ( CApella ) 313.39’3 + 280.51’1= 590.30’4 bulunan değer 360 dereceden büyük olduğu için 360 dereceden çıkar. 590.30’4 – 360= 234.30’4
Ek cetvel 13 e gir 24m sütunundan 37s değerinin karşılığını Aries sütunundan derece olarak bulà
6.10’3 bulunan değeri GHA ya ekle. GHA Dec
06 00 00 234.30’4 N45.59’8
24’37” 6.10’3 Cevap: GHA: 240.40’7 Dec:N45.59’8
Acrux yıldızının GHA ve Dec değerlerinin hesaplanması.
04 Mayıs 1999 01h 25m 10s UT ( GMT ) de, Acrux yıldızının GHA ve Dec değerleri nedir? ( ek cetvel 13 – 38 ve 42 )
Ek cetvel 42 ye gir 4 Mayıs saat 01.00 için aries yıldızının GHA değerlerini al. Aries GHAà 236.28’7
Ek cetvel 42 de Acrux yıldızının SHA ve Dec değerlerini al. Acrux SHAà 173.21’9 – Decà S63.05’9
GHA ( Aries ) + SHA ( yıldız )= 236.28’7 + 173.21’0= 409.49’7 – 360 = 049.49’7 ( değer 360 dereceden büyük olduğu için 360 dereceden çıkarılır.
Ek cetvel 13 e gir Aries bölümünden 25m sütunundan 10s değerini bul. 25mà6.18’5 bulunan değeri GHA ya ekle.
GHA Dec
01 00 00 049.49’7 S63.05’9
25’10” 6.18’5
GHA 056.08’2 S63.05’9 Dec
Venüs gezegeni GHA ve Dec değerleri hesaplanması
04 Mayıs 1999 günü 16h 24m 35s GMT de Venüs ün GHA ve Dec değerleri nedir? ( ekcetvel 13 – 38 – 42 )
Ek cetvel 42 ye gir Venüs sütunundaki 4 Mayıs saat 16.00 karşılıığı değerleri bul. 16 00àGHA 17.05’8 Dec.N25. 43’8, v -0.7, d0.2
Venüs GHA v Dec d
16 00 00 17.05’8 -0,7 N25.43’8 0.2
24m35s 6.08’8
V -0’3 d 0.1
GHA 23.14’3 Dec N25.43’9
Ek cetvel 13 e gir ( güneş gezegen )24m sütunundan 35 saniye değerini bul.24.35sà6.08’8 v -0.7 değerini bulà0.3, d 0.2 değerini bulà0.1 bulunan değerleri GHA ve Dec değerlerine ekle. V değeri (-) eksi olduğu için GHa değerinden çıkarılacak. Cevap: GHA 23.14’3 Dec.N25.43’9
Venüs GHA ve Dec değerlerinin hesaplanması.
04 Mayıs 1999 günü 46.14’00 N – 006.15’00 W DR mevkiinde 06h 24m 22s ZT da Venüs gezegeninden rasat yapıldığında bu gezegenin GHA ve Dec değerleri nedir.( ekcetvel 13 ve 42 )
Çözüm: ZD= 0à GMT= 06h 24m 22s olur.
Ek cetvel 42 ye gir Venüs gezegeninin 4 Mayıs saat 06.00 için GHA, v, Dec, d değerlerini al.
Venüs GHA v Dec d
06 00 00 227.12’4 -0’7 N25.42’0 0.2
24m22s 6.05’5
V 0’3 d 0’1
GHA 233.17’6 Dec N25.42’1
Ek cetvel 13 e gir Güneş, gezegen 24m sütunundan 22s değerini bulà6.05’5, aynı sütundan v -0.7 değerini bulà0.3, d 0.2 değerini bulà0.1. bulunan değerleri GHA ve Dec değerlerine ekle. V nin değeri ( – ) olduğu için GHA dan çıkarılacak. Cevap: GHA:233.17’6 Dec:N25.42’1
Mars gezegeninin GHA ve Dec değerleri hesaplanması.
06 Mayıs 1999 günü 19h 24m 42s GMT de Mars gezegeninin GHA ve Dec değerleri nedir? ( ek cetvel 13 – 38 – 42 )
Ek cetvel 42 ye gir Mars gezegeninin 6 Mayıs sütunundan saat 1900 için GHA, v, Dec ve d değerlerini al.
Mars GHA v Dec d
19 00 00 301.16’3 3.3 S10.34’7 0.2
24m42s 6.10’5
V 1’3 d – 0’1
GHA 307.28’1 Dec S10.34’6
Ek cetvel 13 e gir güneş ve gezegenler 24m sütunundan 42s değer karşılığını bulà 6.10’5, v 3.3 değerini bulà1.3, d 0.2 değerini bulà 0.1. bulunan değerleri GHA ve Dec değerlerine ekle. Zaman arttıkça değer düştüğü için d değeri ( – ) olarak uygulanır. Cevap: GHA 307.28’1 Dec: S10.34’6
Güneşin Meridyen geçişi hesaplanması.
04 Mayıs 1999 günü 44 derece N – 033 derece E mevkiinde bulunan bir gözlemci için Güneş in meridyen den geçiş zamanı UT ( GMT ) olarak kaçtır? ( ek cetvel 07 – 38 )
Ek cetvel 38 e gir Güneşin meridyen geçiş zamanını sağ alt köşeden GMT olarak bulà 11.57 ek cetvel 7 ye gir( 0 – 59 sütunundan ) 33 derece E boylamı için zaman değerini bulà2h 12m bulunan değeri GMT değerinden boylam işareti E olduğu için çıkar. 11.57 – 2.12=09.45 Cevap: 09.45
Güneşin meridyen geçişi hesaplanması.
06 Mayıs 1999 günü 38.00 N – 030.00 W mevkiinde bir gözlemci için Güneş in meridyenden geçiş zamanı UT ( GMT ) kaçtır? ( ek cetvel 7 – 38 )
Ek cetvel 38 e gir Güneşin meridyenden geçiş zamanını sağ alt köşeden GMT olarak bulà 11.57 ek cetvel 7 ye gir ( 0 – 59 sütunundan ) 030 W boylamı için zaman değerini bulà2h00m bulunan değeri GMT değeri ile boylam işareti W olduğu için topla. 11.57 + 2= 13.57. Cevap: 13.57
Ayın üst meridyenden geçişi hesaplanması.
05 Mayıs 1999 günü 37.00 N – 025.00 E mevkiinde bulunan bir gözlemci için Ay’ın üst meridyenden geçiş zamanı UT ( GMT ) nedir? ( ek cetvel 7 – 38 )
Ek cetvel 38 e gir sağ alt köşeden4 ve 5 mayıs için meridyen geçişi değerini alà4 mayısà02.37
5 mayısà03.25 arasındaki zaman farkını bul. 03.25 – 02.37= 00.48’
Ek cetvel 7 ye gir ( 0 – 59 sütunundan ) 25 E boylamı için zaman değeri bulà1h40m
Bulunan değeri boylam işareti E olduğu için 03.25 değerinden çıkar. 03.25 – 01.40= 01.45
Not: cevapta doğru cevap 01.45 gözüküyor. Normalde ek cetvel 8 e girip 2. Çizelgeden boylam değeri ve 48’ değerleri arasındaki düzeltmeyi bulup bulunan değerden boylam işareti E olduğu için çıkarmak gerekir fakat cevap değerlerinde gözükmüyor. 25à48’à4’
01.45’ – 4’= 01.41’ Doğru cevap bu olması gerekir.
Ayın üst meridyenden geçişi hesaplanması.
05 Mayıs 1999 günü 42.00 N – 028 W mevkiinde bulunan bir gözlemci için Ay’ ın üst meridyenden geçiş zamanı UT ( GMT ) nedir?( ek cetvel 7 – 38 )
Ek cetvel 38 e gir sağ alt köşeden 5 ve 6 mayıs için meridyen geçişi değerini alà5 mayısà03.25
6 mayısà04.14 arasındaki zaman farkını bul. 04.14 – 03.25= 00.49’
Ek cetvel 7 ye gir ( 0 – 59 sütunundan ) 28 W boylamı için zaman değeri bulà1h52m
Bulunan değerleri boylam işareti W olduğu için toplaà03.25 + 1.52=05.17
Normalde ekcetvel 8 e girip 2. çizelgeden 28 Wà ve 49’à değerleri arasındaki düzeltmeyi bulup bulunan değere boylam işareti W olduğu için eklemek gerekir.4’ 05.17’ + 4’=05.21’ doğru cevap.
Mars gezegeninin meridyen geçiş zamanı hesaplanması.
06 Mayıs 1999 günü 46.00 N – 052.00 W mevkiinde bulunan bir gözlemci için Mars gezegeninin meridyenden geçiş zamanı UT ( GMT ) nedir? ( ek cetvel 7 – 42 )
Ek cetvel 42 ye gir sağ alt köşeden Mars gezegeninin meridyen geçiş zamanının değerini alà22.59 ekcetvel 7 ye gir ( 0 – 59 sütunundan ) 52 W boylamı için zaman değerini alà3.28 boylam işareti W olduğu için bulunan değerleri topla. 22.59 + 3.28= 26.27à 02h27m 07 Mayıs günü.
Markab yıldızından alınan, Sextant alt 20.14’3 IC +2.5 ve göz yüksekliği 9 m olduğuna göre. Düzeltilmiş yükseklik ( Ho ) nedir? ( ek cetvel 9 )
20.14’3 Sex. Alt
+ 2.5 IC
20.16’8
– 5.3 çevren alçalımı göz yüksekliği düzeltmesi
20.11’3
– 2.6 yıldızların göz yüksekliği düzeltmesi
20.08’9Ho
Ek cetvel 9 a gir 9m için düzeltme değerini bulà-5.3 bulunan değeri çıkar ( – )
20.11.3 ile ek cetvel 9 da yıldızlar ve gezegenler sütununda göz yüksekliği düzeltmesine girà – 2.6
Bulunan değeri işareti ( – ) olduğu için çıkar. Cevap: Ho= 20.08’9
Spica yıldızından alınan Sextant alt 42.38’6 IC: – 1.5 ve göz yüksekliği 15 feet olduğuna göre, düzeltilmiş yüksekli Ho nedir? ( ek cetvel 9 )
42.38’6 Sex.Alt
– 1’5 IC
42.37’1
– 3’8 çevren alçalımı göz yüksekliği
42.33’3
– 1’1 yıldızların göz yüksekliği düzeltmesi.
42.32’2 Ho
Ek cetvel 9 a gir 15 feet için göz yüksekliği düzeltmesini bul. Bulunan değer ( – ) olduğu için çıkar ve bulunan değer ile ek cetvel 9 da yıldız göz yüksekliği düzeltmesine gir. Bulunan değer ( – ) olduğu için çıkar. Cevap: Ho 42.32’2
20 ağustos 1999 tarihinde Venüs gezegeninden alınan Sextant Alt 32.10’, IC: -1 ve göz yüksekliği 6.0m olduğuna göre, düzeltilmiş yükseklik Ho nedir? ( ek cetvel 9 )
32.10’ Sex.Alt
– 1 IC
32.09’
-4’3 göz yüksekliği düzeltmesi
32.04’7
-1.5 yıldızların göz yüksekliği düzeltmesi
32.03.2 Ho
Ek cetvel 9 a gir 6.0 m için göz yüksekliği düzeltmesini bul – 4.3 bulunan değer işareti ( – )olduğu için çıkar. IC değeri ( – ) olduğu için çıkar ve elde edilen değer ile yıldızların göz yüksekliği düzeltme cetveline gir. Bulunan değer işareti ( – ) olduğu için çıkar. Cevap: 32.03’2 Ho
18 Haziran 1999 tarihinde Satürn gezegeninden alınan Sex.Alt 28.40 IC: + 2 ve göz yüksekliği 5.1 m olduğuna göre düzeltilmiş yükseklik Ho nedir? ( ek cetvel 9 )
28.40 Sex.Alt
+ 2 IC
28.42
– 4 göz yüksekliği düzeltmesi
28.38
– 1.8 yıldızları göz yüksekliği düzeltmesi
28.36.2 Ho
Sex.Alt değeri ile IC değerini topla ( + )Ek cetvel 9 a gir göz yüksekliği 5.1 karşılığı düzeltmeyi bulà – 4 bulunan değer ile yıldızların göz yüksekliği düzeltmesine gir ( ek cetvel 9 ) bulunan değer ( – ) olduğu için çıkar. Cevap: Ho 28.36’2
Ayın Alt kenarından alınan Sex.alt 32.20 IC: -2 ve göz yüksekliği 8m olduğuna göre, düzeltilmiş yükseklik Ho nedir? ( HP 54.4 alınacaktır.) ( ek cetvel 9 – 43 )
32.20 Sex.Alt
– 2 IC
32.18
-5 göz yüksekliği düzeltmesi ( 8 m )( ek cetvel 43 de bulunan değer )
32.13
57.9 ek cetvel 43 de 32.13 değer karşılığı bulunan değer
33.10.9
1.2 ek cetvel 43 de HP 54.4 karşılığı 2. Çizelge L sütununda bulunan değer ( +)
33.12.1 Ho değeri
———————————————————————————————————————————-
04 Mayıs 1999 günü 22 00 00 UT ( GMT ) de Ayın üst kenarından alınan Sex.Alt 34.25’0, IC. +1 ve göz yüksekliği 7m olduğuna göre, düzeltilmiş yükseklik Ho nedir? ( HP 54.6 alınacaktır.) ( ek cetvel 7 – 43 )
34.25’0 Sex.Alt
+1 IC
34.26
-4.7 göz yüksekliği düzeltmesi ( 7 m ) ( ek cetvel 43 de bulunan değer )
34.21.3
56.9 ek cetvel 43 de 34.21’3 değer karşılığı bulunan değer.
35.18’2
30’0 Ayın üst kenarından işlem yapıldığı için 30’ düzeltme değeri ( – )
34.48’2
1.8 ek cetvel de HP 54.6 karşılığı 2. Çizelge U sütununda bulunan değer. ( + )
34.50’0 Ho değeri
06 Mayıs 1999 günü Güneş in üst kenarından alınan Sex.Alt 37.28’, IC: +1 ve göz yüksekliği 9m olduğuna göre, düzeltilmiş yükseklik Ho nedir?( ek cetvel 9 )
37.28’ Sex.Alt
+1 IC
37.29
– 5.3 ek cetvel 9 da bulunan 9m göz yüksekliği düzeltmesi
37.23’7
-17.1ek cetvel 9 da bulunan 37.23’7 için mayıs ayı üst kenar düzeltmesi ( – )
37.06’6 Ho
Not: Cevapta 37.06’4 bulunmakta ek cetvel 9 da üst kenar düzeltmesi için ekim – mart düzeltmesinde 37.23’7 karşılığı -17’3 bulunmakta. Onu referans olarak kabul etme durumunda cevap 37.06’4 gözükmektedir. Fakat işlem mayıs ayında olmaktadır.
06 Mayıs 1999 günü Güneşin alt kenarından alınan sextant değeri 46.12’ IC:-2 ve göz yüksekliği 6m olduğuna göre, düzeltilmiş yükseklik Ho nedir? ( ek cetvel 9 )
46.12’ Sex.Alt
– 2 IC
46.10
– 4.3 ek cetvel 9 da bulunan 6m göz yüksekliği düzeltmesi ( – )
46.05’7
+15’1 ek cetvel 9 da mayıs ayı için 46.05’7 karşılığı bulunan değer ( + )
46.20’8 Ho
08 Ağustos 1999 günü Güneşin alt kenarından alınan Sex.Alt 12.20’ IC: -2 ve göz yüksekliği 9 m hava sıcaklığı 40 derece ve hava basıncı 999 milibar olduğuna göre, düzeltilmiş Ho nedir? (ek cetvel 9 – 10)
12.20 Sex.Alt
– 2 IC
12.18
– 5.3 ek cetvel 9 da bulunan 9 m göz yüksekliği karşılığı düzeltme ( – )
12.12’7
+ 11’7 ek cetvel 9 da Ağustos ayıında 12.12’7 için bulunan alt kenar düzeltmesi ( + )
12.24’4
+0’6 ek cetvel 10 da 40 derece ve 999 mb karşılığı M sütunundan bulunan düzeltme (+0.6 ) Göz açısal yükseklik ile girilecek ( 12’24’4 elimizdeki değer.)
12.24’4 + 0’6= 12.25’0 Ho
02 Kasım 1999 günü Güneşin alt kenarından alınan Sex.Alt 8,42’ IC – 2 göz yüksekliği 4.2 m hava sıcaklığı -20 derece ve hava basıncı 980 mb olduğuna göre, düzeltilmiş yükseklik Ho nedir?( ek cetvel 9 ve 10 )
8.42’ SexAlt
– 2’ IC
8.40
-3.6 ek cetvel 9 da 4.2m için bulunan göz yüksekliği değeri ( – )
8.36’4
+10.8 ek cetvel 9 da bulunan alt kenar için düzeltme 8.36’4 karşılığı yok. 9.34’ karşılığı alındı.
8.47’2
– 0.8 ek cetvel 10 da bulunan -20 C 980 mb ve 8.47’2 göz açısal yüksekliği değeri.
8.46’4 Ho
Not cevap 8.45’9 olması gerekir. Soru cevabı yanlış çünkü ek cetvel 9 da 8.36’4 değerinin karşılığı yok. Soru hatalı. Örnek olması açısından yapıldı.
02 Mayıs 1999 günü göz yüksekliği 18 feet olan bir seyirci 10 00 00 GMT de Ay ın üst kenar yüksekliğini 32.46’7 olarak ölçmüştür. Gözlem anında hava sıcaklığı 20 C ve hava basıncı 990 mb dır. Düzeltilmiş sextant yüksekliği Ho nedir? ( ek cetvel 10 – 39 – 43 )
32.46’7 Ayın üst kenarı
-4’1 18 feet göz yüksekliği karşılığı bulunan düzeltme ( – )
32.42’6
+0.1 hava sıcaklığı 20 C ve 990 mb J bölümünden bulunan düzeltme ( + )
32.42’7
57’7 Ayın üst kenarı için düzeltme ek 43 32.42’7 karşılığı ( + ) ek cetvel 43 da bulunacak.
33.40’4
30’0 Ayın üst kenarından yapılan işlem sonucu indirilmesi gereken dakika değeri
33.10’4
2 Mayıs saat 10 00 00 da Ayın HP si 54.0; HP 54.0 karşılığı düzeltme 54.0à U sütunuà 1.5
33.10’4
+ 1.5 HP 54.0 karşılığı ek cetvel 43 de U sütununda bulunan düzeltme.
33.11’9 Ho Cevap
03 Mayıs 1999 günü göz yüksekliği 48 feet olan bir seyirci IC değeri +2’7, fabrikasyon hata değeri +0’1 olan bir sextant ile akşam rasat zamanı Venüs yüksekliğini 50.19’9 olarak ölçmüştür. Venüs ün düzeltilmiş Ho değeri nedir? ( ek cetvel 9 )
50.19’9 Venüs yüksekliği
+2’7 IC değeri
50.22’6
+0’1 fabrikasyon hata değeri
50.22’7
– 6’7 ek cetvel 9 da 48 feet yüksekliği bulunan düzeltme değeri. ( – )
50.16’0
– 0’8 ek cetvel 9 dan bulunan 50.16’0 karşılığı göz yüksekliği değeri ( – )
50.15’2 Ho
04 Mayıs 1999 günü göz yüksekliği 18m olan bir seyirci, Güneşin üst kenarından yaptığı ölçüm sonucu yüksekliği 63.41’4 olarak tespit etmiştir. IC değeri +1’2, ölçüm anında hava basıncı 970 mb ve hava sıcaklığı 20 F olduğuna göre, düzeltilmiş sekstant yüksekliği nedir? ( ek cetvel 9 ve 10 )
63.41’4 Güneş üst kenarı
+1’2 IC değeri
63.42’6
– 7’5 ek cetvel 9 da bulunan 18 metre göz yüksekliği karşılığı düzeltme ( – )
63.35’1
0’0 ek cetvel 10 970 mb 20 F karşılığı düzeltme ( E sütunundan) ( – / + 0)
63.35’1
-16’3 ek cetvel 9 da 63.35’1 karşılığı bulunan üst kenar düzeltmesi ( – )
63.18’8 Ho
Yatay ve düşey sextant açısı ile mesafe hesabı.
Yatay sextant açısı ile formül: Mesafe=( 57.3 x haritadan ölçülen genişlik ) / Derece olarak sextant.
1.Düşey sextant açısı ile formül: Mesafe değeri feet olarak verilmişse;
Mesafe = ( 0.565 x haritadaki madde yüksekliği ( feet ) / maddenin dakika olarak sextant düşey açısı.
-
Düşey sextant açısı ile formül: Mesafe değeri metre olarak verilmişse;
Mesafe= (1.854 x haritadaki madde yüksekliği ( metre ) / maddenin dakika olarak sextant düşey açısı.
Bir gemi seyir anında adanın sextant la iki ucu arasındaki açıyı 7 derece ölçmüştür, adanın haritadan ölçülen genişliği 1’.7 mildir. Geminin adadan olan mesafesi nedir?
Formül: Mesafe= ( 57.3 x haritadan ölçülen genişlik)/ derece olarak sextant.
Cevap: 57.3 x 1’.7=97.41 / 7 = 13.91 mil. Mesafe: 13.91 mil.
Bir gemi seyir anında adanın düşey açısını sextant ile 5.36’ derece ölçmüştür. Haritada aynı tepenin yüksekliği 250 feet tir. Geminin adadan olan mesafesi nedir?
Cevap: 1 derece sektant açısı= 60’ – 5 x 60= 300’ – 300’ + 36’= 336’ eder.
Formül: Mesafe=( 0.565 x haritadaki madde yüksekliği ( feet ) / maddenin dk. Olarak sextant düşey açısı.
( 0.565 x 250 ) = 141.25 – 141.25 / 336’= 0’.42 Cevap: 0’42 mil.
Bir gemi seyir anında adanın düşey açısını sextant ile 3.36’ derece olarak ölçmüştür. Haritada aynı tepenin yüksekliği 300 feet tir. Geminin adadan olan mesafesi nedir?
Cevap: 1 derece sektant açısı= 60’ – 3 x 60= 180’ – 180’ + 36’= 216’ eder.
Formül: Mesafe=( 0.565 x haritadaki madde yüksekliği ( feet ) / maddenin dk. Olarak sextant düşey açısı.
( 0.565 x 300 ) = 169.5 – 169.5 / 216’ = 0’78 mil.
Bir gemi seyir anında bir adanın iki ucu arasındaki mesafeyi sextant ile 10 derece olarak ölçmüştür. Adanın haritadan ölçülen genişliği 2 mildir. Geminin adadan olan mesafesi nedir?
Formül: Mesafe= ( 57.3 x haritadan ölçülen genişlik ) / derece olarak sextant
Mesafe: ( 57.3 x 2 )= 114.6 – 114.6 / 10 = 11’46 mil. Cevap: 11’46 mil
Bir gemi seyir anında bir adanın iki ucu arasındaki mesafeyi sextant ile 5 derece olarak ölçmüştür. Adanın haritadan ölçülen genişliği 1 mildir. Geminin adadan olan mesafesi nedir?
Formül: Mesafe= ( 57.3 x haritadan ölçülen genişlik ) / derece olarak sextant
Mesafe: ( 57.3 x 1 )= 57.3 – 57.3 / 5 = 11’46. Cevap: 11’46 mil
Bir gemi seyir anında adanın düşey açısını sextant ile 2.54’ derece ölçmüştür. Haritada aynı tepenin yüksekliği 300 m dir. Geminin adadan olan mesafesi nedir?
Maddenin düşey yüksekliği metre olarak verilmişse formül şöyledir.
Mesafe= ( 1.854 x haritadaki madde yüksekliği ( metre ) / maddenin dakika olarak sextant düşey açısı.
2.54’= 2 x 60’ = 120’ – 120’ + 54’ = 174’
Mesafe= ( 1.854 x 300 )556.2 – 556.2 / 174 = 3’196 = 3’2 mil eder. Cevap: 3’2 mil
Seyir halinde bir geminin boyu 300 feet. Pruvadan bırakılan yüzer bir cismin 10 saniye sonra pupadan geçtiği saptanmıştır. Geminin sürati nedir?
1 feet= 30.48 cm 300 x 30.48 = 9144 cm / 100 = 91.44 m.
1 saat = 60 dakika. 60 dakika= 3600 saniye.
1 mil= 1852.3m
10 saniyede 91.44 metre gittiğine göre 3600 saniyede ne kadar yol alır.
3600 x 91.44/ 10= 32918.4/ 1852.3= 17.77 Cevap: 17.77
Bir geminin pruvasında pupasına kadar olan mesafe 367.5 feet olduğuna göre, pruvadan bırakılan yüzer bir cismin 14 saniye sonra pupadan geçtiği saptanmıştır. Geminin sürati aşağıdakilerden hangisidir?
1 feet= 30.48 cm 1 saat = 60 dakika. 60 dakika= 3600 saniye. 1 mil= 1852.3m
367.5 x 0.3048= 112.014 m
14 saniyede 112.014 m ise 3600 saniye de ne kadar yol alır.
3600 x 112.014 / 14 =28803.6 m. Gider. 28803.6/ 1852.3= 15’55 mil Cevap: 15’55 mil.
Bir filikanın süratini belirlemek için filikanın baş tarafından yüzer bir cisim denize atılıyor, cisim filikanın baş ve kıç bodoslamalarından geçerken zaman tespiti yapılıyor ve süre 18 saniye olarak bulunuyor. Filikanın boyu 28 kadem olduğuna göre filikanın saatteki hızı nedir?
1 kadem= 30.48 cm. 1 saat = 60 dakika. 60 dakika= 3600 saniye. 1 mil= 1852.3m
28 x 0.308=8.5344
18 saniyede 8.5344 m giderse 3600 saniyede ne kadar yol alır.
8.5344 x 3600 / 18 = 1706.88 m gider.
1706.88 / 1852.3 = 0.92 mil Cevap: 1 saatteki hızı 0’92 mil
10 knot ile ilerleyen bir tekne şamandıralara yakın seyrederken, bir şamandırayı görmesi ile kaybetmesi arasındaki süreyi 10 dakika olarak belirlemişse görüş mesafesi kaç mildir?
Cevap: 60’ da 10 mil giderse 10’ da ne kadar mil görmüştür.
10 x 10 = 100 – 100 / 60 = 1’666 mil görmüştür.
1.666 / 2 =0’83. Cevap: Görüş mesafesi 0’83 mildir.
Zaman hesapları:
26 Ekim günü 40.00 N – 117.19’4 W boylamında, Notik almanaktan güneşin doğuşu 06.58 olarak bulunmuştur. Anılan boylamda güneş ZT olarak saat kaçta doğacaktır.
Cevap: 120 – 117.19’4= 2.40’6 = ( 6×6=36” ) 2 derece 8 dakika eder.
1 derece60mil ve 1 derece 4 dakika ettiğine göre 40 x 4 /60=2.666 – 2 x 60 =40 = 2’40”
8’ + 2’40”=10’40” – 06.58’00” – 10’40”= 06.47’20” Cevap: 06.47’20”
088 W boylamında ZT 16.55 iken LMT değeri nedir?
090 – 088 = 2 x 4 = 8 dakika. 16.55 + 00.08= 17.03
10.42’36” E boylamındaki bir mevki ile 36.16’24” E boylamındaki bir mevki arasındaki zaman farkı nedir?
Cevap: 36.16’24” – 10.42’36” = 25.33’48” ( doğuya gidildiği için koordinat değerleri ( – )
25 x 4 =100 / 60’=1.666 – 1.666 – 1 x 60 =40’ = 1 h 40m.
1 derece 60 mil. 1 derece 4’ zaman farkı olduğuna göre 33’ x 4’ / 60’=2.2 – 2.2 – 2 x 60=12” = 2’12”
1.40’+2’12”= 1.42’12” 1.42’12” + 0.00’02”= 1.42’14” Cevap: 1.42’14”
60’= 4 30’ = 2’ 15’ = 1’ 00’ = 0’ 60” = 0.4”
48” x 0.4” / 60”=0.32 – ( 0.32 – 0 x 60”= 19’2 = 2” ) 2 saniye.
20.15’36” boylamında olan bir mevki ile 42.28’18” W boylamında olan bir mevki arasındaki zaman farkı nedir?
Cevap: 42.28’18” + 20.15’36”=62.43’54” ( doğudan batıya gidildiği için koordinat değerleri + )
62 x 4’ = 4. 133 – ( – 4 x 60=8 ) = 4h 08m.
1 derece 60 mil. 1 derece 4’ zaman farkı olduğuna göre 43’ x 4’ / 60=2.866 – ( -2.866 x 60 = 52”) =2’52” 4h 08m + 2m 52s= 4h 10m 52s +0.00.02 = 4h.10m54s Cevap: 4h 10’56”
60’= 4 30’ = 2’ 15’ = 1’ 00’ = 0’ 60” = 0.4”
54” x 0.4”/ 60”=0.36 ( 0.36 -0 x60 =2”) veya 1’ x 2’ / 30’= 0.066 – 0 x 60= 4”
05 Mayıs 1999 tarihinde Greenwich hakiki zamanı GAT 19.34’20 ise UT (GMT) nedir?(ek cetvel 38)
Ek cetvel 38 gir sağ alt köşede sol sütunda zaman denklemi bölümünden 5 mayıs için değeri bulà03.15
Bulunan değeri eldeki GAT zamanı ile topla ( + ) 19.34’20 + 3’15= 19.37’35 Cevap: 19.37’35
05 Mayıs 1999 günü saat 10.24’ UT ( GMT ) de, Greenwich hakiki zamanı nedir?( ek cetvel 38 )
Ek cetvel 38 e gir sağ alt köşede zaman denklemi bölümünden sağ sütunda 05 mayıs için değeri bulà03.17
Bulunan değeri eldeki Greenwich zamanından çıkar. ( – ) 10.24’ – 03’17”= 10.20’43” Cevap:10.20’43”
115 W mevkiinde güneşin batışı LMT olarak 16.48’00” bulunmuştur. Güneş batış zamanı Zt olarak kaçtır?
Cevap: 120 – 115 = 005 5 x 4=20’ 16.48’00” – 28’ = 16.28’00” Cevap:16.28’00”
Boylamı 060.12’ W olan bir mevkide LMT 08h21m37s iken boylamı 018.03’ olan bir noktada LMT kaçtır?
Cevap: 060.12’ + 018.03’= 78.15’ 78 x 4 / 60 =5.2 -5 x 60= 12’ = 5h 12m
15’ x 4’/ 60’= 1’ 5h 12m + 1m= 5h 13m Cevap: 08h 21m 37s + 5h 13m= 13h 34m 37s
15 Aralık günü güneş 36.27’ N – 072.30’ E mevkiinde GMT olarak 20.30 da batmıştır. LMT olarak güneşin batış saati nedir?
Çözüm: 72 x 4 =288 288/60=4.8 -4 x 60=48’ 4h 48m
30’ x ‘4 / 60’=2’ 4h 48m + 2m= 4h 50m 20h 30m + 4h 50m= 01h 20m ( 16 aralık )
Seyir halindeki bir gemiden 26 mayıs günü ZT 16h34m14s de güneşten rasat yapılmıştır. DR boylamımız 156.19’5 E dir. Rasat yapıldığı andaki GMT nedir?
156 x 4 / 60=10.4 veya 156 / 15=10.4 16h 34m 14s – 10h= 06h 34m 14s
7,5 0 7,5 22.5 37.5 52.5 67.5 82.5 97.5 112.5 127.5 142.5 157.5 172.5
– 1 – 2 – 3 – 4 – 5 – 6 -7 – 8 – 9 -10 -11
Seyir durumundaki bir gemi 26 Nisan günü Zone time olarak 16h 36m 14s de güneşten rasat yapmıştır. Rasat anındaki DR mevkiin boylamı 159.19’5 E dir. Rasat yapıldığı anda GMT zamanı nedir.
Cevap: 16h 34m 14s – 11h= 05h 36m 14s
38.41’ N 125.20’ W olan bir A mevkiinde 21 Ağustos 2003 tarihinde vardiya saati 13.15 ise 55.17’N 082.45’ E mevkiinde bulunan bir gözlemci için vardiya saati kaçtır?
+127.5+112,5 +97.5 +82.5 +67.5 +52.5 +37.5 +22.5 7.5 0 -7.5 -22.5 -37.5 -52.5 -67.5
+8 +7 +6 +5 +4 +3 +2 +1 -1 -2 -3 -4
-82.5 -97.5
-5 -6
Aradaki zaman farkı 14 saat olduğuna göre 13.114=27.15 27.15 – 24.00= 03.15 22 Ağustos.
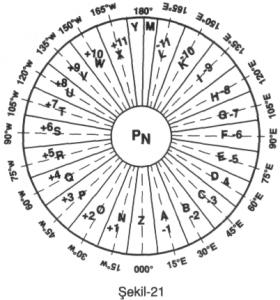
DOĞU YARIM KÜRESİ
(ZD) Saat Farkı:-l -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12
Bölge Harfi :ABCDEFGHIKL M
Standart Zaman
Boylamı : 15°E 30°E 45°E 60°E 75°E 90°E 105°E 120°E 135°E 150°E 165°E 172°,5 E -180°
V
ts)
oo
BATI YARIM KÜRESİ
Saat Farkı :+1 +2 +3+4+5 +6 +7 +8 +9 +10 +11 +12
Bölge Farkı :NOPQRSTUVWX Y
Standart Zaman
Boylamı : 15°W 30°W 45°W 60°W 75°W 90°W 105°W 120°W 135°W 150°W 165°W 172°,5 W-180°
Greenwich Sıfır Bölgesi Z
Bölgesel saatler belirtilirken bölge (ZONE) harfi vaktin sonuna konmalıda-. Örneğin 63° 35′ E boylamındaki bölge saatine göre saat 15h 30m 20S belirtmek için 15h 3GP 20S D olarak yazılmalıdır. Burada kullanılan D harfi, belirtilen vaktin hangi bölge saatine göre olduğunu gösterdiği gibi, GMT bulmak için saat farkının (Zone Discription’ın) ZD-4 olduğunuda belirtir.
(ZONE TIME) ZT 18h35m42sD ZT 15h 42m 30S Q
Bölgesel Saatin ZD -_4 ZD +4
GMT Dönüştürülmesi: GMT 14h 35m 42S GMT19h42m30s
x

Yay parçasını veya boylamı zamana değiştirmek için kural; derece, dakika. ( x ) ve saniyeleri 15 e böl çıkan değeri ( – ) yani saat, dakika veya saniyeyi çıkar kalan küsuratı 60 ile çarp.
Örnek: 68 derece 52’ 35”
68/15=4.533 saat -4 x 60=32’
52’/15=3.466 dakika -3 x 60=28”
35”/15=2.333 saniye -2 x 60=20 salise bulunan değerleri topla.
4h 32m
3m 28s
2s20salise
+———————–
4h35m30s2salise eder.
Zamanı boylama veya açıya değiştirmek için kural; Saatleri 15 ile çarp ( x ), dakika ve saniyeleri 4 e böl ( / ) çıkan değeri ( – ) yani dakika ve saniyeyi çıkar kalan küsuratı 60 ile çarp.
Örnek:
8h58m27s
8×15=120 derece
58/4=14.5 derece -14×60=30’ dakika
27/4=6.75 dakika -6×60=45” saniye. Bulunan değerleri topla
120 derece
14.30’
6’45”
+—————-
134.36’45” bulunur.
GMT=ZD – ZT dır. MERKEZ BOYLAM = ZD x 15°
ZD rakamını bilmek, seyirciye; bulunduğu bölgenin, bölge zamanını (ZT) bulmasında
yardımcı olur.
ÖRNEK : Boylamı: 127° 13’2 W
Boylamı: 127° 42’4 W olan mevkilerin bölge tanıtma (ZD) rakamları nedir ?
Çözüm: 127°13’2/15 = 8 kalan 7°,5 den küçük (7°13’2) bu durumda ZD = +8 dir.
127°42’2/15 = 8 kalan 7°,5 den büyük (7°42’4) bu durumda ZD = +9 olur.
GMT ile ZT arasındaki ilişki
Astronomik Seyirde gök cisimlerinin koordinatlarını bulurken gereksinme duyduğumuz
zaman ZT den çok GMT dir. Zira almanakta verilen bilgiler GMT zamanına göredir.
ÖRNEK
-
BÖLGE ZAMANI (ZT) VE YEREL ZAMAN (LMT) ARASINDAKİ İLİŞKİ :
LMT; bölge zamanından, bölgenin merkez boylamından itibaren, doğuya veya batıya
doğru olan boylam farkının (dlo) zaman cinsinden değeri kadar bir farklılık gösterir. Notik
almanaklarda bütün göksel olaylar (alaca karanlık, doğuş ve batış ve boylam geçiş zamanları)
orta boylama göre ve LMT zamanı olarak verilmiştir. Eğer seyirci merkez boylamın doğusunda
ise, göksel olaylar merkez boylamından önce oluşur. Bu hususun hiçbir zaman unutulmaması
gerekir. Göksel olayın ZT olarak hesaplanabilmesi için almanaktan bulunan LMT değerine
boylam farkının zaman değeri ilave edilir veya çıkartılır. (Merkez boylamın doğusunda ise
çıkartılır, Batısında ise toplanır). Aşağıdaki örnekte Güneş’in doğuş zamanının ZT olarak
bulunuşu gösterilmiştir.
Büyük daire seyri;
Başlangıç rota açısı 38 derece başlangıç noktası koordinatları 47 derece N – 050 derece W olan bir büyük daire seyri için vertex noktasına mesafe nedir? ( ek cetvel 26 )
Cevap: LHA 38 olur. Ek cetvel 26 ya gir. 47 derece sütunundan en büyük Hc değeri alà sütundan alınması gereken bilgiler. Dec – Hc – d – Z
Decà54 en büyük Hcà 65.10’3 d -1’9 Z 59.1’
Mesafeyi bulmak için; 90 – Dec
Vertex başlangıç noktasına olan mesafeyi bulmak için 90 – 54=36 derece bulunan dereceyi dakikaya çevir. 36 x 60’=2160 mil eder. Cevap.2160 mil
Kalkış noktası 51.N – 065 W varış noktası 40.37’ N – 010.00’W olan bir büyük daire seyri için kalkış rota açısını ve mesafeyi bulmak için NP 401 in ilgi sayfasına girilerek aşağıdaki değerler elde edilmiştir.
( ek cetvel 28 )
Hc d Z
48.32’6 +28.6 81.2
Ekte bulunan interpolation cetvelini kullanarak mesafeyi bulun.
Çözüm; Enterpolasyon cetveline d değeri olan 28.6 değeri ile girilir.
Dec.Inc 20’ Decimals ……8’
28.6 9.5 .6 4.1
Sonra double second corr. Sütunundan 28.6 için düzeltme bulunur. ( 28.0 – 29.6 arasında ) 1.8
Sonra enterplasyon tablosundan bulunan bütün değerleri topla.
TTL= 9.5 + 4.1 + 1.8=15.4 ve mesafeyi hesaplamaya geç.
Distance: 90 – Hc + TTL Distance= 90 – 48.32’6 = 41.27’4 + 15.4= 41.42’8=2502.8 mil bulunur.
Kalkış noktası 51.N – 065 W, varış noktası 61 N – 005 W olan bir büyük daire seyri için kalkış rota açısı ve mesafe aşağıdakilerden hangisidir? ( problem ekte bulunan NP 401 sayfası kullanılarak çözülecek.)
( ek cetvel 27 )
Çözüm: LHA= dlongà65W -5W = 60 ek cetvel 51 derece sütunundan Lat2= dec 61 dereceye gir.
51 derece
Dec Hc d Z
61 56.19’9 10’2 49.2
Kalkış rota açısı= N 49.2 E= 49.12’
Mesafeyi bulmak için; Distance= 90 – Hc x 60 90 – 56.19’9= 33.40’ 33 x 60=1980 + 40=2020 mil
Kalkış noktası 46 derece N – 065 W varış noktası 50 derece N – 027 W olan bir büyük daire seyri için kalkış rota açısı ve mesafeyi bulun. ( problem ekte bulunan NP 401 sayfası kullanılarak çözülecek. Ek cetvel 26 )
Çözüm: LHA yı bulmak için dlong bulunur. Dlong= 65W – 27W= 38 derece bulunur.
Ek cetvel LHA 38 derece ile girilir ve Dec sütunundan 50 derece nin karşılığı ve46 derece sütunundaki değerler bulunur. Lat 2 = Dec.
46 derece sütunu
Dec Hc d Z
50 64.32’6 +4’9 67.0’
Kalkış rotası= Z değeri 67.0’ işareti ise N ve E dir. Kalkış rotası N 67 E
Mesafeà Dist= 90 – Hc 90 – 64.32’6= 25.27’4 25 x 60=1500 + 27=1527 mil bulunur.
Kalkış noktası 48 N – 050 W ve kalkış rota açısı N60 E olan bir büyük daire seyri için vertex noktasının koordinatları nedir? ( problem ekte verilen NP 401 sayfası kullanılarak çözülecek.) ( ek cetvel 27 )
Çözüm: LHA 60 olur. Ek cetvel 27 de 48 derece sütunundan gir ve en büyük Hc yi bul.
48 derece
Dec Hc d Z
66 54.35’1 -1’1 37.4’ bulunur.
Vertex noktasının koordinatları Lat= Hc ve Long = Long1 – Z değeridir. Bu durumda çözüm.
Lat. 54.35’1N ( yani Hc değeri ) Long = 050W – 37’4Z= 12.36’ W
Cevap: Lat: 54.35’1N Long:12.36’W
Kalkış noktası koordinatları 45 derece N – 060 W, vertex noktası koordinatları 52.12’7 N – 023 18 W, kalkış rota açısı 60 derece olan bir büyük daire seyrinde, vertex noktasından sonraki ilk ilk ara noktanın koordinatları nedir? ( Ara noktalar yaklaşık 5 derece dlong farkı ile alınacak ve ekteki NP 401 sayfası kullanılarak problem çözülecektir.)( ek cetvel 27 )
LHA= 60 ek cetvel ile 45 derece sütununa gir. Vertex noktası karşılığı Dec değerinden 5 derece önceki Hc değerini bul.
45 derece
Dec Hc d Z
60 52.06’4 -3’9 44.8
65 52.12’7 -2’8 36.7
Vertex noktasından sonraki ilk ara nokta koordinatları Dec 60 değerinde görülen Hc değeridir.
Lat= Hc long= Long1 – Z. Long= 60 – 44’8= 15.12’W dir Cevap: 52.06’4 N – 15’12 W
Enlem – Boylam ve mesafe hesaplamaları
40’00’ N – 026 W mevkii ile 35’40 N – 023’20 W mevkii arasındaki deprature kaç mildir?
Çözüm: Dist= dlong x Cos MLat.
Dlong= 026.30’ W – 023.20’ W = 03.10’ 3 x 60’=180’ 180’ + 10’ = 190’
MLat= 40.00’ N + 35.40’ N = 75.40’ 75.40’ / 2 = 37.50’
Dist= 190 x Cos37.50’= 150’73 mil eder.
42.10’ N – 036.20’ E mevkii ile 46.20’ N – 033.00’ E mevkii arasındaki departure kaç mildir?
Çözüm: Dist= dlong x Cos MLat.
Dlong= 036.20’ E – 033.00’ E = 03.20’ 03 x 60’= 180’ + 20 = 200’
MLat= 42.10’ N + 46.20’ N = 88.30’ 88.30’ / 2 = 44.15’
Dist= 200 x Cos44.15 = 143.5 mil
36.20’ N – 040.20 E mevkii ile 36.20’ N – 044.40’ E mevkii arasındaki mesafe yaklaşık kaç mildir?
Çözüm: Dist= dlong x cosMlat
Dlong= 044.40’ – 040.20’ = 4.20’ 4 x 60’= 240’ 240’ + 20’ = 260’
Mlat= 36.20’ + 36.20’ = 72.40’ 72.40’ / 2 = 36.20’
Dist= 260’ x Cos36.20’= 209’8 mil
120 rotasına 100 mil seyrederek 40.0 N – 020.0’ mevkiine demirleyen bir geminin seyre kalktığı mevkiinin enlemi nedir?
Çözüm: 180 -120 = 60
Dlat= Dist x Cos60 100’ x Cos60 = 50’
Kalkış enlemimiz Lat A kuzeyden güney istikametine olduğu için 40.50’ N olur. Cevap: 40.50’ N
Göksel seyir
ZD +4 ( W ) olan bir saat diliminde ve 32 enlemindeki bir mevkide ZT 04 00 00 iken LMT 04 30 00 ise be mevkiin boylamı nedir?
Çözüm: GMT= ZT – / + ZD = 04.00.00 + 4= 08 00 00 GMT:08.00.00 LMT= GMT – Long W 04.30.00= 08.00.00 – Long Wà Long W= 03.30.00
03.30= ( 3 x 15 ) + ( 0,5 x 55)
45 + 7.5 = 52.5 = 52.30’ bulunur.
5 derece E boylamı üzerinde bir mevkide ZT 08.15 iken GMT nedir?
Çözüm: GMT= ZT – ZD = 08.15 – 0 = 08.15 GMT
ZD – 4 olan bir saat diliminde ve 32 N enlemindeki bir mevkide ZT 14. 00. 00 iken LMT 14.15.00 ise, bu mevkiin boylamı nedir?
Çözüm: GMT= 14.00.00 – 4 = 10.00.00 GMT bulunur.
LMT= GMT – Long E 14.15.00 = 10.00.00 – Long E Long E = – 04.15 saat.
04.15= ( 4 x 15 ) + ( 0,5 x 15 ) 60 + 7.5= 67.5 = 67.30’ Cevap: 67.30’
115 W mevkiinde güneşin batışı LMT olarak 16.48.00 bulunmuştur. Güneşin batış zamanı ZT olarak kaçtır?
LMT= GMT + Long Wà 16.48= GMT + 115W / 15)à GMT=24.28 bulunur.
GMT= ZT – / + ZD 24.28 – 8= 16.28 ZT= 16.28 bulunur.
Veya 120 – 115 =5 5 x 4= 20’ 16.48’- 20’= 16.28 ZT
Boylam 060.12’ W olan bir mevide LMT 08.21.37 iken boylamı 018.03 E olan bir noktada LMT kaçtır?
Çözüm: boylamları topla 4’ ile çarp 60 a böl 60 78 x4 = 5.2 -5 x 60= 12 = 5h12m
Boylamdaki dakikaları topla 12’ + 03’ = 15 15 X 4 =60 60 / 60=1’ dakika.
5h 12m + 1m=5h 13m W den E e giderken toplanır 08 h 21m 37s + 5h 13m= 13h 34m 37s bulunur.
Bir gök cisminin almanaktan bulunan GHA değeri 220 derece, Dec 15.00 N ve DR mevkiin koordinatları 35 N – 060 E olduğuna göre HA ( t ) açısı nedir?( Boylam E GHA ile topla )
Çözüm: HA= 360 – ( GHA – / + Long ) 360 – ( 220 + 60 ) = 80 derece bulunur. HA( t ): 80 derece
Boylamımız 100 W ve GHA değeri 350 ise saat açısı ( HA veya t ) nedir?
Çözüm: ( boylam W GHA dan çıkar ) HA= 360 – ( 350 – 100 )= 110 derece olur. HA ( t ): 110 derece
GHAy değeri 242 ve SHA H değeri 103 ise GHA H değeri nedir?
Çözüm: GHA H = GHAy + SHA H = 345 olur.
Kutup yıldızının düzeltilmiş açısal yüksekliği ( Ho ) 51. 15’ – a0; 14’8 a1; 0’6 a2; 0’6 olduğuna göre bulunduğunuz enlem değeri nedir?
Çözüm: 51.15’ + 14’8 + 0’6 – 1 = 50.30’4 ( emin değilim )
Vardiya zabiti olarak güneşin batış anında semtini 289 olarak ölçtüğünüze göre, güneşin o andaki SİA değeri nedir?
280 – 270 = 019 bulunur.
Semt açımız güneşin batı için W Semt> 270 olduğuna göre N işareti alır. Cevap: N019 W
Vardiya zabiti olarak güneşin doğuş anında semtini 079 derece olarak ölçtünüz. Güneşin o andaki Sİa değeri nedir?
Çözüm: SIA= 090 – 079 = 11 derece işareti ise E ve N olur.
Cevap: N11E
Geminizin mevkii 28.00’S – 42.36’W dir. Güneş in Dec değeri N 20.30’ SİA değeri 23.4 dür. Güneşin doğuşunda semti nedir?
Çözüm: SIA = 90 – Semtà Semt= 90 – SIA SEMT= 90 – 23.4= 66.6 SEMT: 66.6 olur.
03 Mayıs 1999 günü 09.24.22 UT ( GMT ) de Güneşin GHA ve Dec değerleri nedir? ( Ek cetvel 13 – 39 )
Çözüm:
Güneş GHA Dec d
09 00 00 315.46’3 N15.35’2 0.7
24 22 6.05.5 d 0.3
GHA 321.51.8 Dec N15.35.5 Cevap: GHA:321.51.8 Dec:N15.35.5
Fenerlerin coğrafi görüş mesafesini hesaplamak:
Değer feet olarak verilmişse; Formül= ( 1.14 x harita yükselliği karesi ) + 1.14 Köprü üstü yüksekliği karesi)
Örnek: Gp Fl ( 2 ) 10 Sec 81 feet olan 10M özelliğindeki bir feneri, 16 feet göz yüksek olan bir zabitin feneri coğrafi olarak görme mesafesi nedir?
Çözüm: 81 karesi 9 16 karesi 4 ( 1.14 x 9 ) + 1.14 x 4 )à ( 10.26 ) + ( 4.56 )=14.82 mil eder
Harita ve Köprü üstü mesafesi metre olarak verilmişse; Formül=
Görüş mesafesi= ( 2.08 x Harita yüksekliği karesi ) + ( 2.08 x Köprü üstü yüksekliği karesi )
Örnek: Göz yüksekliği 25 metre olan bir fener göz yüksekliği 16 metre olan bir gözlemci tarafından kaç milden görünür?
Çözüm: 25 karesi 5 16 karesi 4 ( 2.08 x 5 ) + ( 2.08 x 4 )à( 10.4 ) + ( 8.32 )=18.72 mil eder.
Haritada bir fenerin yüksekliği 225 feet, 49 feet lik bir görüş mesafesi olan bir köprü üstünden coğrafi görüş mesafesi nedir?
Değer feet olarak verilmişse; Formül= ( 1.14 x harita yüksekliği karesi ) + 1.14 Köprü üstü yüksekliği karesi)
Çözüm: 225 karesi 15 49 karesi 7 ( 1.14 x 15 ) + ( 1.14 x 7 )à ( 17.1 ) + ( 7.98 )=25.08 mil eder
Haritada bir fenerin yüksekliği 225 metre, 49 metre lik bir görüş mesafesi olan bir köprü üstünden coğrafi görüş mesafesi nedir?
Görüş mesafesi= ( 2.08 x Harita yüksekliği karesi ) + ( 2.08 x Köprü üstü yüksekliği karesi )
Çözüm: 225 karesi 15 49 karesi 7 ( 2.08 x 15 ) + ( 2.08 x 7)à ( 31.2 ) + ( 14.56 ) 45.76 mil eder
Göz yüksekliği 64 feet olan bir gözlemci için 144 feet yüksekliğindeki bir feneri kaç milden görebilir?
Değer feet olarak verilmişse; Formül= ( 1.14 x harita yüksekliği karesi ) + (1.14 Köprü üstü yüksekliği karesi)
Çözüm: 64 karesi 8 144 karesi 12 ( 1.14 x 8 ) + ( 1.14 x 12 )à ( 9.12 ) + ( 13.68 )= 22.8 mil eder
Kutup seyri:
80 N 040 E mevkiinde hakiki yön 150 derece ise grid yönü nedir?
Grid yönü= Hakiki yön ( – / + long ) ( +W / – E )à Kuzey kutbu.
Formüle göre boylam işareti E olduğu için ve Kuzey kutup ta bulunulduğu için boylam değeri hakiki yön değerinden çıkarılacak. 150 – 40 = 110 derece
82 S – 010 W mevkiinde hakiki yön 040 derece ise grid yönü nedir?
Grid yönü= Hakiki yön ( – / + long ) ( + E / – W )à Güney kutbu.
Formüle göre boylam işareti W ve Güney kutupta bulunulduğu için boylam değeri hakiki yön değerinden çıkarılacak. 040 – 010 = 030 derece
79 N – 130 W mevkiinde grid rotası 045 ise hakiki rota kaçtır?
Grid yönü= Hakiki yön ( – / + long ) ( + W / – E )à Kuzey kutbu.
Formüle göre boylam işareti W ve Kuzey kutupta bulunulduğu için boylam değeri ve rota toplanacak
130 + 45 = 175 derece
80S – 050E mevkiinde grid rotası 120 ise hakiki rota kaçtır?
Grid yönü= Hakiki yön ( – / + long ) ( +E / -W ) à Güney kutbu.
Formüle göre boylam işareti E ve Güney kutupta bulunulduğu için boylam değeri rota ile toplanacak.
120 + 50 = 170 derece
Pusula ve Kerteriz hesaplamaları:
C D M V T yöntemi:
C; Manyetik pusula rotası ve kerterizi ( Compass &Bearing )
D; Arizi sapma veya yapay sapma ( Deviation )
M; Magnetik rota veya kerteriz ( Magnetic &Bearing)
V; Doğal sapma ( Variation ) ( Haritadaki pusula gülünde okunan değer.)
T; Hakiki rota veya kerteriz ( türe course & Bearing )
Bu yöntemde dikkat edilecek konu Soldan sağa doğru gidilirken E değerler ( + ) W değerler ( – ) olur.
Sağdan sola gidilirken W değerler ( + ) E değerler ( – ) olur.
Örnek: Manyetik pusulamız ile 112 dereceye ilerlerken bölgede doğal sapma değeri 2 derece E ve bu rotadaki yapay sapma 4 derece W ise hakiki rota nedir?
C:112 D:4W M? V:2E T:?
C D M V T
112 – 4W 108 2E+ 110 Cevap: 110 derece true course ( Hakiki rota ) bulunur.
Ana cayro pruva değeri 078 derece iken ripiter pruva değeri 080 olarak yanlış devreye alınmış bir ripiterle A fenerinin kerterizi 268 olarak alınıyor. Ana cayro hatası 3 E olduğuna göre hakiki kerteriz kaç derecedir?
Çözüm: Ripiter hatası : 80 – 78= 2 W A fenerinin gerçek kerterizi= 268 – 2 W= 266
Cayro hatası= 3 E Hakiki kerteriz: 266 + 3= 269 derece.
Bu soru C D M V T olarak soldan sağa işlemi olarak şöyle yapılır.
C : 268 ( A fenerinin kerterizi ) D: 2 W ( Burada ana cayro değeri > ripiter değeri ise W olur.
Ana cayro değeri< Ripiter değeri ise işaret E olur.
M:? V: 3 E T:?
C D M V T
268 – 2W 266 3E + 269 Cevap: 269 derece.
Güneşin meridyenden geçiş anında filika pusulasının yapay sapmasını belirlemek isteyen filika amiri filika pusula kart merkezine bir kalemi dik tutarak gölgesinin 190 derece çizgisinin üstüne düştüğünü belirlemiştir. Bölgede doğal sapma 3W olduğuna göre o andaki pruva derecesi için yapay sapma miktarı nedir?
Çözüm: Soruda Güneşin meridyenden geçişi sırasında dediği için True ( T ) 180 olur.
C D M V T
190 ? ? 3W 180
C D M V T
190 7W+ 183 3W+ 180ß Cevap: yapay sapma 7W
14 Ocak 2003 seyir yaptığımız bölgeye ait haritanın pusula gülü üzerinde 0.35’ ( 1981 ) 5’W ibaresi olan bulunmaktadır. Manyetik pusula ile 225 rotasına seyrederken bu rotadaki yapay sapma değeri 4 derece W ise gemimizin hakiki rotası nedir?
Variation hesabı: 2003 – 1981=22 yıl 22 x 5= 110 110= 1 derece 50 dk W 1.50 – 0.35= 1.15 W bulunur.
C D M V T
225à4 Wà 221à 1.15Wà219.45 bulunur.
20 Ocak 2003 tarihinde seyir yapılan bölgede bulunan iki burnun transiti harita üzerinde 055 dir. Aynı transit geminin manyetik pusulası ile 065 olarak ölçüldü. Haritanızın pusula gülü üzerinde 3.20 W (1985) 5’ W ibaresi var. Manyetik pusulanın yapay sapması ne kadardır?
Variation hesabı: 2003 – 1985=18 yıl 18 x 5 =90 90= 1.30 W eder. 3.20 W + 1.30 W= 4.50
Variation= 4.50 W
C D M V T
065 5.10W 59.50 4.50W 055ß sağdan sola gidilince W işaretliler toplanacak (+) Cevap:5.10W
Kerteriz problemleri:
İskele tarafımızdaki bir cisimden Nispi kerteriz alırsak; Formül; Hakiki kerteriz – rota
Sancak tarafımızdaki bir cisimden Nispi kerteriz alırsak; Formül; Nispi kerteriz + rota.
Hakiki kerteriz kuzeyden itibaren saat yönü istikametinde 000 – 360 derece arasında ölçülür. Nispi kerteriz geminin pruvasından itibaren Sancak / İskele ye doğru 1 – 180 derece arasında ölçülür.
Örnek: A gemisinin rotası 135 derece olup B gemisi sancak 35 derece de kerteriz edilmiştir. B gemisinin hakiki kerterizi nedir?
Cevap: 35 + 135=170 derece
Rotası 070 olan A gemisinin vardiya zabiti B gemisini İskele 40 derecede kerteriz etmektedir. B gemisi vardiya zabiti ise A gemisini iskele 110 derecede kerteriz etmektedir. Bu durumda B gemisinin rotası nedir?
Çözüm: A gemisi B gemisini Hakiki = 070 + 40 = 110 da kerteriz ediyor.
B Gemisi A gemisini Hakiki = 030 + 180= 210 da kerteriz ediyor.
B gemisinin rotası: 210 + 110=320 bulunur.
262 rotasına seyreden bir A gemisinin hakiki olarak 082 de gördüğü B gemisinin nispi kerterizi nedir?
Çözüm. Hakiki kerteriz= Nispi kerteriz ( – / + ) rota. Bu soruda A gemisi 262 ye giderken 082 hakiki kerterizde B gemisini gördüğüne göre; B gemisi A gemisinin kıç tarafındadır.
082= Nispi Kerteriz + 262 Nispi kerteriz= 262 – 82 = 180 Nispi kerteriz 180 derece bulunur.
172 rotasına ilerleyen bir gemiden 150 derece hakiki kerterizinde bulunan bir fenerin nispi kerterizi kaç derecedir?
172 rotasına giderken fener 150 derece hakiki kerteriz edilmiş. Buna göre fener iskele taraftadır.
150= Nispi kerteriz – 172 Nispi kerteriz= 150 – 172=22 derece iskelede bulunur.
Veya Nispi kerteriz = 360 – 022= 338 derece bulunur. Bu soru cevabı 338 dir.
Rotası 340 derece olan bir A gemisi B gemisini Sancak 85 de görmektedir. B gemisi A gemisini hakiki kaç olarak görmektedir?
Çözüm: A gemisi Hakiki kerterizi= Nispi kerteriz + rota
A gemisi Hakiki kerterizi= 85 + 340 425 -360= 65
B gemisi Hakiki kerterizi= 180 + 65= 245 B gemisi hakiki kerterizi 245 bulunur.
Rotası 040 olan bir A gemisi B gemisini İskele 70 de görmektedir. B gemisi A gemisini hakiki kaç derece görür?
Çözüm: A gemisi hakiki kerterizi= 040 – 70=30 360 – 30= 330
B gemisi hakiki kerterizi: 330 – 180= 150 bulunur.
Rotası 340 olan bir A gemisi B gemisini sancak 60 derece görmektedir. B gemisi A gemisini hakiki kaç derecede görür?
Çözüm: A gemisi hakiki kerterizi : 60 + 340= 400 400 – 360= 040
B gemisi hakiki kerterizi= 180 + 40= 220 derece bulunur.
Sahildeki bir fenerin cayro ripiterinden alınan kerteriz 310 derecedir. Geminin hakiki mevkiinden bu fenerin haritadan ölçülen kerterizi 308 derecedir. Cayro hatası nedir?
Çözüm. CE= Haritadan ölçülen kerteriz – ripiterden ölçülen kerteriz. İşareti – ise W, + ise E olur.
CE= 308 – 310= -2 -2 bulunur. İşareti ( – ) olduğu için W olur. Cevap: 2 W
Atlantik okyanusunda 156 rotasına seyrederken karşılaştığınız cayro hatası 0 olan bir gemi ile yapmış olduğunuz pusula kontrolünde, siz gemiyi 356 da kerteriz ettiniz. Diğer gemi sizi 179 da kerteriz ettiğini bildirdiğine göre. Cayro pusula hatanız nedir? Önce pusula hatası 0 olan gemiye göre rota bulunur. 179 + 180= 359 C.E= 359 – 356= 3 derece bulunur. İşareti + olduğu için E dir. Cevap: 3E


